Solving Equations by Factoring
Using Factoring to Solve Equations
How is factoring useful in solving equations? Consider, for
example the factored equation
(3x - 2)( x + 1) = 0.
To solve this, use the following important principle.
Zero Product Property
For all numbers a and b, if ab = 0, then a = 0, b = 0, or both
a and b equal 0.
Since (3x - 2)( x + 1) = 0, then the Zero Product Property
states that either 3x - 2 = 0, x + 1 = 0, or both equal zero.
| 3x - 2 = 0 |
or |
x + 1 = 0 |
| 3x = 2 |
|
x = -1 |
 |
|
|
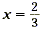So, the solutions of (3x - 2)( x + 1) = 0 are 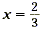and x = -1. Now apply
this property to solve an equation that must be factored first.
Example 1
Find the solutions of 2x 3 -2x 2 = 12x .
Solution
First, write this equation so that it is set equal to zero.
| 2x 3 - 2x 2
- 12x = 0 |
|
| x ( 2x 2 - 2x -
12 ) = 0 |
Since x is a factor of all the terms,
factor it out. |
| 2x ( x 2 - x - 6
) = 0 |
Since each coefficient is even, factor
out a 2. |
Now factor x 2 - x - 6 as a product ( x + a )( x +
b ) for some values of a and b.
| ( x + a )( x + b ) |
= x 2 + ( a + b )x + ab |
| |
= x 2 - x - 6 |
In other words, a + b = -1 and ab = -6. By looking at the
factors of -6, we see that a = 2 and b = -3 satisfy these
requirements. So x 2 - x - 6 = ( x + 2)( x - 3). (Check
to see if this is correct by multiplying it out.)
| 2x ( x 2 - x - 6
) = 0 |
|
| 2x( x + 2)( x - 3) = 0 |
Substitution |
Use the Zero Product Property to find the solutions.
| 2x = 0 |
x + 2 = 0 |
x - 3 = 0 |
| x = 0 |
x = -2 |
x = 3 |
So, the solutions of the equation are x = 0, x = -2, and x =
3.
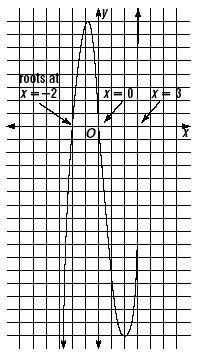
Finally, point out that the solutions of the equation are the
roots (zeros) of the function
y = 2x 3 - 2x 2 - 12x.
Graphically, the roots are where the graph of the function y =
2x 3 - 2x 2 - 12x intersects the x -axis. Plot
some points or use a graphing calculator to graph this function.
The roots are at x = 0, x = -2, and x = 3, as shown on the
figuer below.
