Slope

Objective Learn how to find the slope of a line.

 

Steepness and Slope

You surely have some vague idea of what is meant by slope. For instance, the slope of a roof, an up-hill road, or a ladder. We will assign a number that allows us to measure the steepness of a straight line. The greater the absolute value of the number is, the steeper the line will be.

 

Definition of Slope

The picture below shows two straight lines, each containing two points.

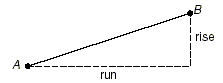
There are two numbers associated with each pair of points, namely the rise and the run.

The rise is the vertical difference between point B and point A , and the run is the horizontal difference between point B and point A . You should note that the differences may be negative.

Definition of Slope The slope is the quotient .

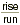Let’s apply this concept to a line on the coordinate plane.

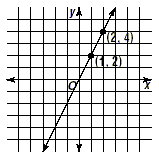
Notice that the line contains the points whose coordinates are (1, 2) and (2, 4). To find the slope of the line, you must first determine the rise. To do this, calculate the difference of the y -coordinates. The rise is 4 - 2 or 2. Next, determine the run. To do this, calculate the difference of the corresponding x-coordinates. The result is 2 - 1 or 1. Therefore, the slope is the quotient

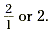
Let’s choose two different points that lie on the line, say (0, 0) and ( -1, -2).

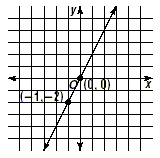
Find the slope.

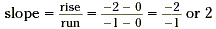
Notice that the slope is the same for any pair of points on the same straight line. This means that we may speak of the slope of a line without referring to a particular pair of points.

 

Slope and Parallel Lines

Graph the lines given by y = 2x, y = 2x + 1, y = 2x + 2, y = 2x + 3, y = 2x - 1, y = 2x - 2, and y = 2x - 3.

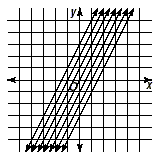
Next, determine the slopes of these lines. They should find that all of the lines have a slope of 2. What can you say about the lines?

The lines are parallel.

Key Idea Two lines in a plane are parallel if they never meet.

Look at the family of graphs shown on the coordinate plane. If we select any two different lines, they will never intersect because they “stay the same distance apart” as we move up or down along the lines. The following key idea can be concluded from this example.

Key Idea Two lines are parallel if and only if they have the same slope.

 

Exercises

Complete each of the following.

1. Tell whether the lines given by 2x + 3y = 5 and 4x + 6y = 9 are parallel. Explain.

Since the lines have the same slope, they are parallel.

2. Are the lines given by y = 3x + 4 and y = 3x + 2 parallel? Why or why not?

Yes; they have the same slope.

3. Suppose we are given two lines. The first contains the points whose coordinates are (1, 2) and (4, 7). The second contains the points whose coordinates are (0, 0) and (5, 8). Are these lines parallel? Explain.

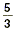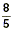The slope of the first line is , and the slope of the second line is . Since the slopes are not equal, the lines are not parallel.