Product and Quotient of Functions
We can also form new functions by multiplying or dividing.
Definition — Product and Quotient of Two Functions
Given two functions, f(x) and g(x):
The product of f and g, written (f · g)(x), is defined as
(f · g)(x) = f(x)
· g(x).
The domain of (f · g)(x) consists of all real numbers that are in the
domain of both f(x) and g(x).
The quotient of f and g, written
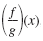 , is defined as , is defined as
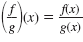 Here g(x)
≠
0. Here g(x)
≠
0.
The domain of
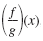 consists of all real numbers that
are in the domain of both f(x) and g(x) and for which g(x)
≠ 0. consists of all real numbers that
are in the domain of both f(x) and g(x) and for which g(x)
≠ 0.
Example 1
Given f(x) = 8x - 5 and g(x) = x2 + 6x, find the product (f
· g)(x).
Solution
| Multiply the functions. Substitute for f(x) and g(x).
Multiply.
Combine like terms.
So, (f · g)(x) = 8x3 +
43x2 - 30x. |
(f · g)(x) |
= f(x) · g(x)
= (8x - 5) · (x2 + 6x)
= 8x3 + 48x2 - 5x2 - 30x
= 8x3 + 43x2 - 30x |
To multiply two binomials, use FOIL
(First, Outer, Inner, Last).
That is,
(a + b)(c + d) = ac + ad + bc + bd.
Example 2
Given f(x) = x2 - 11x + 30 and g(x) = x2 - 25, find the quotient
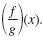
Solution
Note:
To factor x2 - 11x + 30, find two integers
whose product is 30 and whose sum is -11. They are -5 and -6.
To factor x2 - 25, find two integers whose
product is -25 and whose sum is 0. They
are -5 and 5.
|