Adding Triangular Numbers
1 Adding Two Consecutive Triangular Numbers
One interesting result from triangular numbers is that the sum
of two consecutive numbers is a perfect square. In fact, if T
n represents the n th triangular number, then T n-1
+ T n = n 2.
Example:
Let T n represent the n th triangular number. Find T 7
+ T 8 .
Since we are adding the seventh triangular number to the
eighth triangular number, we need to compute the square of 8. 8 2
= 64 and thus, T 7 + T 8 = 64. You could
verify that T 7 = 28 and T 8 = 36 and then
add 28 + 36 = 64.
T 7 + T 8 = 64.
2 Adding a Series of Triangular Numbers
To add a series of triangular numbers starting with 1, you
need to first find the index of the triangular number is used
last. For example, if we were adding 1 + 3 + 6 + 10, then the
index of the last number is 4, because we are adding up to the
fourth triangular number. The sum of these triangular numbers is
given by the formula with the index equal to n:
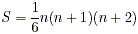
In fact, these numbers are called tetrahedral numbers.
Example:
1 + 3 + 6 + 10 + 15 + 21 + 28 =
We are adding up to the seventh triangular number. Setting n =
7 and applying the formula above, we get
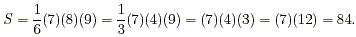
Therefore, 1 + 3 + 6 + 10 + 15 + 21 + 28 = 84.
|