Slope
Definition of Slope
Words The slope is the value of the quotient 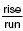 . .
Model
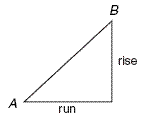
Interpretation of the Slope
Draw three lines whose equations are y = x , y = 2 x , and 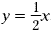 . These lines look like this in the coordinate plane. . These lines look like this in the coordinate plane.
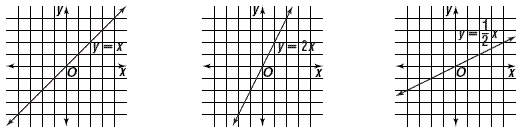
Check the slopes of each of the lines. Note that the line with
largest slope of 2 is the steepest, and that the line with least
slope of 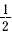 is the least steep. is the least steep.
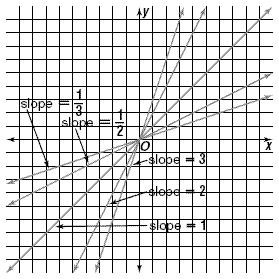
The figure above shows lines of various slopes.
Slopes of Horizontal and Vertical Lines
"What slope should a horizontal line have?"
Since a horizontal line always has rise equal to zero, the
slope will always be zero divided by a positive number, and so
the slope is zero. Note that the x-axis has zero slope.
"What about vertical lines?"
Since the run is always zero and division by zero is
undefined, the slope is undefined. It is sometimes useful to
think of them as having "infinite slope," but since
infinity is not a number, this is not a precise statement.
Negative Slope
Notice that so far all slopes have been positive numbers, and
all lines have sloped upward from left to right. For lines drawn
in the coordinate plane, the standard direction to move along
them is from left to right and bottom to top.
Key Idea
Lines with positive slope rise to the right and lines with
negative slope rise to the left.
- For positive slopes, the larger the number, the more
steeply the line slopes upward.
- For negative slopes, the larger the absolute value of the
negative number, the more steeply the line slopes
downward.
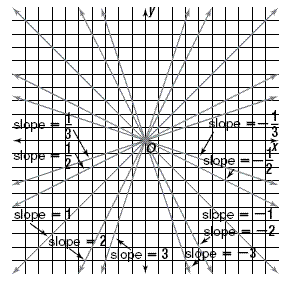
The next figure shows lines of both positive and negative
slopes.
Algebraic Formula for Slope
Let's summarize the whole discussion by introducing the
algebraic formula for slope. To do this, we draw two points in
the coordinate plane that correspond to the ordered pairs (x
0 , y 0) and (x 1 , y 1),
as in the figure below.
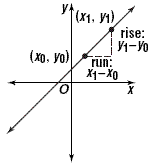
The rise is y 1 - y 0 and the run is x
1 - x 0 . Slope is rise divided by run, which
gives the formula
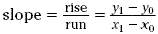
Values can be substituted into this formula once the
coordinates are given. It does not matter which points are
designated as (x 0 , y 0) and (x 1
, y 1). However, the first x in the denominator must
come from the same coordinate pair as the first y in the
numerator.
|