Solving Simple Equations
The aim of this document is to provide a short, self
assessment programme for students who wish to acquire a basic
competence at solving simple equations.
In this section we shall look at some simple equations and the
methods used to find their solution. There are four basic rules:
Rule 1 An equal quantity may be added to both
sides of an equation.
Rule 2 An equal quantity may be subtracted
from both sides of an equation.
Rule 3 An equal quantity may multiply both
sides of an equation.
Rule 4 An equal, non-zero quantity may divide
both sides of an equation.
The application of these rules is illustrated in the following
examples.
Example
Solve the equations
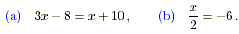
Solution
(a) By Rule 1 we may add 8 to both sides:
3 x - 8 + 8 = x + 10 + 8 i .e. x = x + 18.
By Rule 2 we may subtract x from both sides:
3 x - x = x + 18 - x i .e. 2 x = 18.
Finally, by Rule 4 we may divide both sides by 2 giving x = 9
.
(b) By Rule 3 we may multiply both sides by 2,
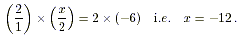
It is always good to check that the solution is correct by
substituting the value into both sides of the equation. In
Example 1 (a), by substituting x = 9 into the left hand side of
the equation we see that x - 8 = 3 × 9 - 8 = 19. Substituting x
= 9 into the right hand side of the equation gives x + 10 = 9 +
10 = 19. Since both sides of the equation are equal when x = 9,
it is a correct solution. In this case it is the only solution to
the equation but it is important to note that some equations have
more than one solution.
Exercise
(a) 3 x = 18 , (b) 7 x = -14 (c) -2 x = -10 (d) 28 x = 35 (e)
5 x - 3 x - 12 x = 29 - 2 - 7 (f) 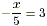
Solution
(a) Dividing both sides by 3 gives
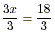
or x = 6 .
(b) Dividing both sides by 7 gives
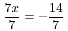
or x = - 2 .
(c) Dividing both sides by - 2 gives
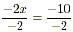
or x = 5 .
(d) Here 7 is the highest common factor of 28
and 35. First let us divide both sides by this.
28 x = 35
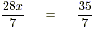
4x = 5
Now divide both sides by 4.
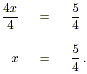
The solution is thus x = 5 / 4 .
(e) First let us simplify both sides. The
left hand side is
5 x - 3 x - 12 x = 5 x - 15 x = - 10 x .
The right hand side is
29 - 2 - 7 = 29 - 9 = 20 .
The original equation is thus - 10 x = 20
and the solution to this is obtained by dividing both sides of
the equation by - 10.
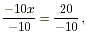
so that x = - 2 .
(f) In this case we must multiply both sides
by 5.
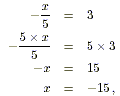
and the solution in this case is x = - 15 .
Try the following short quizzes.
Quiz 1
Which of the following is the solution to the equation
8 x + 5 x - 3 x = 17 - 9 + 22 ?
(a) 2 (b) -2 (c) 3 (d) -3
Solution:
Simplify both sides first:
8 x + 5 x - 3 x = 13 x - 3 x = 10 x .
17 - 9 + 22 = 8 + 22 = 30 .
The equation to be solved is thus 10x = 30 and this clearly
has solution x = 3 .
Quiz 2
Which of the following is the solution to the equation
x - 13 x = 3 x - 6 ?
(a) 2 5 (b) - 1 5 (c) 1 3 (d) - 6 17
Solution:
x - 13 x = 3 x - 6
- 12 x = 3 x - 6 .
0 = 12 x + 3 x - 6
15 x - 6 = 0
15 x = 6
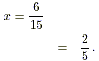
|